Every month, the magazine ORMS Today features an Operations Research related puzzle called "The PuzzlOR" by John Toczek, available online here. I always find these pretty fun, and October's puzzle was no exception.
Here was the question last month:
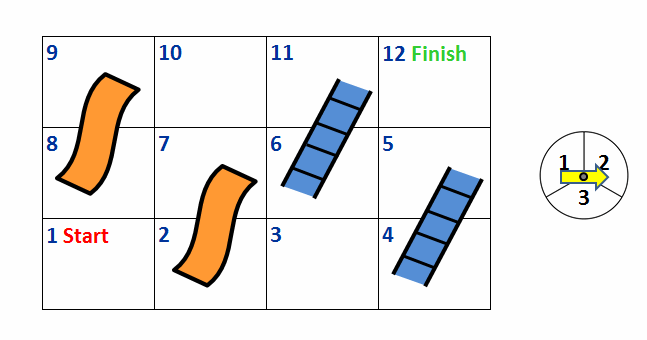
Chutes and Ladders is a popular children’s game where players compete to move along a game board the fastest. It involves both hazard squares that can set you back a few spaces and some helpful squares that can move you forward a few spaces. A mini version of the game is displayed in Figure 1.
A player starts at the red “Start” square and finishes at the green “Finish” square. A player advances along the board by spinning a spinner that results in moving forward one to three squares.
If a player ends his turn on a Ladder (depicted by the blue ladder icon) he immediately moves upwards along the ladder. For example, if a player ends his turn on square 6, he would immediately move to square 11.
If a player ends his turn on a Chute (depicted by the orange slide) he immediately moves down the slide. For example, if a player ends his turn on square 7, he would automatically move to square 2.
A player wins the game when he lands on or passes the Finish square.
Question: What is the average number of turns needed to finish the game? (Please provide your answer with one decimal place.)
It's pretty well known that chutes and ladders can be modeled as an absorbing Markov Chain. Given the rules of the game and the board layout, we can create a transition matrix that shows the probability of moving from any transient state to any other state.
In an absorbing Markov Chain, there exists at least one state such that we never leave once we get to it. This is called the absorbing state. In chutes and ladders, the absorbing state is the 'finish' — once you finish the game you don't go back to the transient states. Normally, chutes and ladders has a ton of different states, making it pretty tedious to construct the transition matrix. But this puzzle is nice because it creates a small and simple enough version that we can set up the transition matrix by hand.
For instance, when we start at the first box of the game (labeled "1" in the image), the spinner gives us the following transition probabilities:
- 1/3 chance of moving to box 2.
- 1/3 chance of moving to box 3.
- 1/3 chance of moving to box 4, immediately taking the ladder, and ending in box 5.
- 0 chance of ending up in any other state.
We can actually do this for any of the boxes on the board. In doing so, one thing becomes immediately obvious — you can never end up in a state which is the beginning of a chute or ladder. That means that there are actually only 8 states we can be in: 1 ("start"), 2, 3, 5, 6, 8, 10, 11, 12+ ("finish"). For ease of use, let's just call these states 0 through 7.
Let's construct an 8x8 matrix $P$ representing all of the possible transitions, where the element $P_{ij}$ represents the probability from moving from state $i$ to state $j$:
import numpy as np
np.set_printoptions(precision=2)
# define the transition matrix
P = np.array([[0, 1/3., 1/3., 1/3., 0, 0, 0, 0],
[0, 0, 1/3., 2/3., 0, 0, 0, 0],
[0, 0, 0, 2/3., 0, 0, 1/3., 0],
[0, 1/3., 0, 0, 1/3., 0, 1/3., 0],
[0, 0, 0, 0, 1/3., 1/3., 1/3., 0],
[0, 0, 0, 0, 0, 0, 1/3., 2/3.],
[0, 0, 0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 0, 0, 1]], dtype=np.float64)
print P
Now that we have the whole game modeled, there are two ways to figure out the "average number of turns needed to finish the game."
Solving analytically¶
Absorbing Markov Chains are often represented as follows:

Here, the matrix $P$ is divided up between transient states $Q$, probabilities of being absorbed from each of those states $R$, a $\boldsymbol{0}$ matrix representing the fact that you will never go back from an absorbed state, and an identity matrix $I$ representing the fact that once a process is absorbed it stays absorbed (the probability of going from an absorbed state to itself is 1).
# find the fundamental matrix N
Q = P[:-1, :-1]
I = np.eye(7)
N = np.linalg.inv(I - Q)
# find mean steps until absorption -- we only care about the first element
# since the rules say we always start in the first state
print N.dot(np.ones(7)).ravel()[0]
So on average it takes about 5.2 moves to get from the starting state to finishing the game.
Simulating¶
Another way to figure this out is to simulate many runs through the game and see empirically how many moves it took to finish. Here's a function that simulates playing the game:
def move(state, P):
"""
Execute one transition from the current state, returns new state.
state -- an int representing the current state
P -- transition matrix
"""
possible = P[state, :].nonzero()[0]
probs = P[state, possible].cumsum()
return possible[probs >= np.random.rand()].min()
def play_chutes_and_ladders(P):
"""
Play a game of chutes and ladders, return the number of moves.
P -- transition matrix
"""
# initialize the game
state = 0
moves = 0
while state < 7:
state = move(state, P)
moves += 1
return moves
# run a bunch of simulations and find out the average number of moves
N = 100000
results = np.array([play_chutes_and_ladders(P) for _ in xrange(N)])
print 'mean moves to finish', results.mean()
Once again we find an average of about 5.2 moves.
If you enjoyed reading about this problem, you can read more about Markov Chains here. Here's another PuzzlOR which is similar but based on Monopoly instead of chutes and ladders.